Measuring Up Metric

Some common prefixes used in the metric system are also used in technology. The photos will help students who are not familiar with the prefixes.

Paraphrase:

• You may already be familiar with these powerful prefixes. Can you determine their meanings from reading these science phrases?

As you go through each prefix, ask students to think of other words that have the same prefix.

Here are a few examples:

• mega – a large quantity (megaplex, megaphone, megabucks)
• nano – extremely small (nanosecond)
• micro – tiny (microchip, microphone)
• giga – a very large number (gigantic). You may want to point out the difference in pronunciation.

At the bottom of the page, there are computer-related examples of how these prefixes are used. They will help students understand why we use prefixes when talking about very large numbers.

​

This section introduces additional prefixes in the metric system, building off of students’ understanding of how mega-, nano-, micro-, and giga- are used to describe size.

Paraphrase:

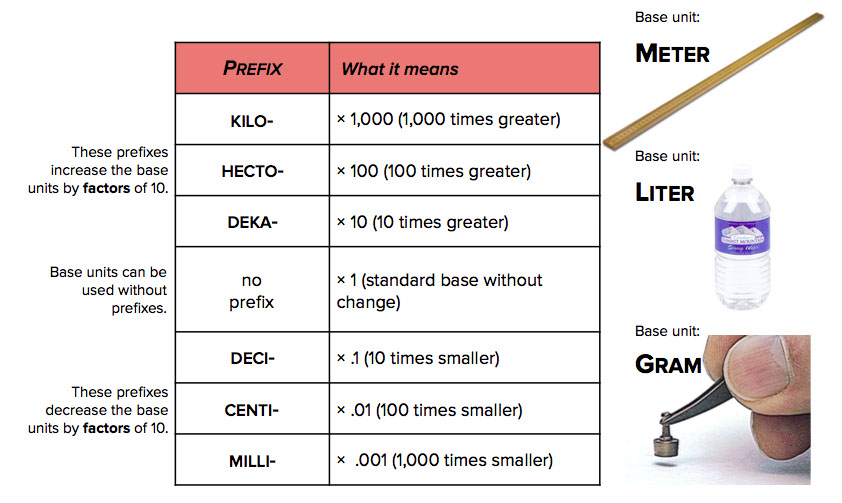
• A tremendous feature of the metric system is that once you learn the three base units, you can use the prefixes to scale them to whatever you need to measure.
• The metric prefixes are associated with specific quantities. Ask students what they notice about the quantities. They should notice that they are all in multiples of 10.
• The base units for length (meter), volume (liter), and mass (gram) are also provided.

Have students complete the activity at the bottom of the page. They must determine the appropriate terminology for each measurement task. Remind students that they may consult the chart at the top of the page.

Note: There is some ambiguity regarding volume measurements. Discuss this with students. For example, cubic units are used to measure volumes too. More about this later, though.

​

Answers

• Meters are helpful for measuring the height of a building, but centimeters are better for measuring a book.
• Kilograms are helpful for measuring the mass of a human, but grams are better for measuring the amount of salt in a recipe.
• Liters are helpful for measuring beverages, but milliliters are better for measuring a dose of cough syrup.

In the conversation between two friends on the running track, one who is obviously learning the metric system and practicing converting units. You may have kids read this allowed chorally, with one group reading the blue balloons and the other reading the yellow balloons.

​

Students scale units within the metric system, along with a practice item. The first three are examples of scaling, with diagrams showing how the decimal points move.

When scaling down (i.e. using a smaller unit to measure, such as meter to centimeter), the decimal point moves to the right.

When scaling up (i.e. using a larger unit to measure, such as centimeter to meter), the decimal point moves to the left.

Students may use the chart from the Prefixes and Conversions section above as a resource throughout the unit.

"Your turn!" Answer:

• 1250 milliliters

​

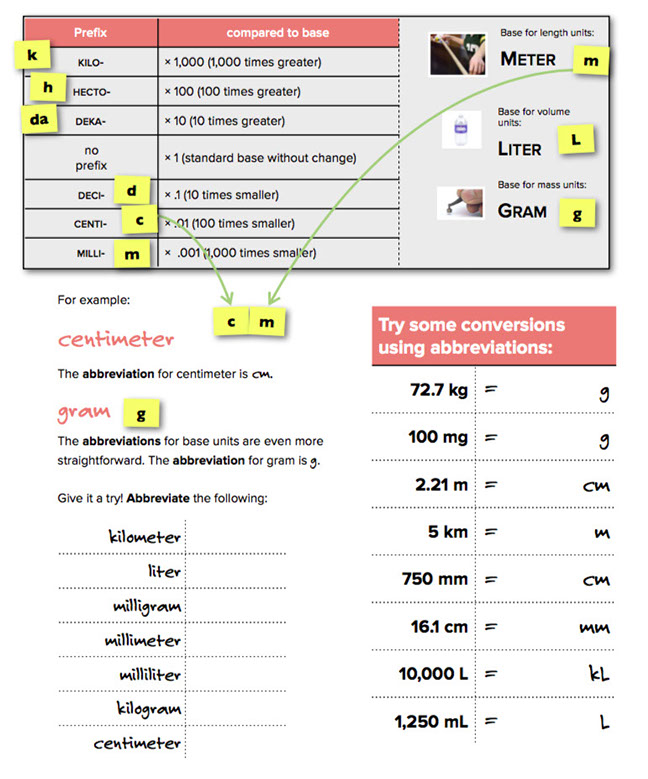
This chart shows students the abbreviations that are used to express measurements using the metric system. They are recognized throughout the world.

Have students fill in the abbreviations of the more common metric units of measurement in the exercise on the left.

For the first answer, students may have heard of a "5K run." This is actually 5 km. This is an abbreviation of an abbreviation!

Answers:

• kilometer = km
• liter = L
• milligram = mg
• millimeter = mm
• milliliter = mL
• kilogram = kg
• centimeter = cm

Next, ask students to practice scaling using the abbreviations (the exercise on the right). They can refer to the prefix chart if they need to.

Answers:

• 72.7 kg = 72,700 g
• 100 mg = .1 g
• 2.21 m = 221 cm
• 5 km = 5000 m
• 750 mm = 75 cm
• 16.1 cm = 161 mm
• 10,000 L = 10 kL
• 1250 ml = 1.25 L

Scientific Language Practice

Explain to students that, when writing a metric unit, the metric abbreviation is never made plural by adding an "s." However, when saying a metric unit, it is necessary to add the s. That is, we never write "kms" but we do say "kilometers."

Also, instruct students to use the word point to express a decimal. For example: “seventy-two point seven kilograms equals seventy-two thousand seven hundred grams.”

​

A Brief Overview of Metric Abbreviations

The metric system also has a convenient set of abbreviations that is recognized all over the world.

To use the system, join together a prefix abbreviation and a base abbreviation.