SciGen Teacher Dashboard
Unit E3
Delivering Power to the People
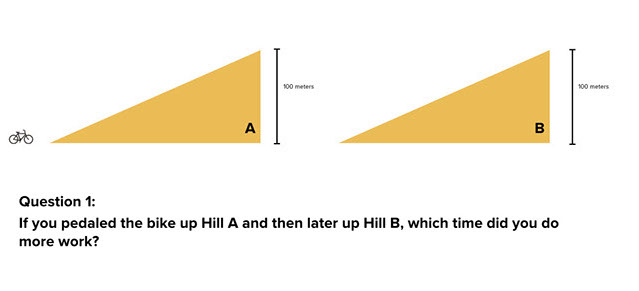
Pedal Power
More About Power—Biking Uphill
Energy Transformations
Electricity Generation
Power Priorities
 Lesson: More About Power—Biking Uphill
Lesson: More About Power—Biking Uphill
Duration: Approximately 60 minutes
Students crunch the numbers for biking uphill to learn more about power. Students consider questions about biking up a steep slope, and then learn how to calculate the work and power behind. Along the way they practice use of the focus words and learn which units we use to calculate power (joules and watts, for example).
LEARNING OBJECTIVE
Students continue to explore and apply scientific language relating to power. Students practice using this important vocabulary and scientific terminology.
Students discuss questions with their partners and try to reach an agreement.
Teacher Tips
- To poll the students en masse, use different colors of paper or distinct hand signals to represent the different answers. For example, you can ask the students to use rock, paper, and scissors to indicate their answers.
Teacher Tune-ups
Teaching Notes
ACTIVITY OVERVIEW
- Three questions to discuss (20 minutes)
- Remember newtons and joules? (15 minutes)
- Introduce watt (15 minutes)
- Apply power concept to other situations (10 minutes)
Three questions to discuss (20 minutes)
Students are asked to consider the work and power required to pedal a bike up two identical hills. The first question asks which hill requires more work. (In this scenario, the rider took 1 minute to climb the first hill and 2 minutes to climb the second). The second question asks which hill required the most power.
Give students a moment to answer the first multiple-choice question (about work) before reading on to the provided answer.
Have students talk to their partner and agree on an answer for the second multiple-choice question (about power). Read the "reveal" paragraph that explains that more power was used on the first hill.


Remember newtons and joules? (15 minutes)
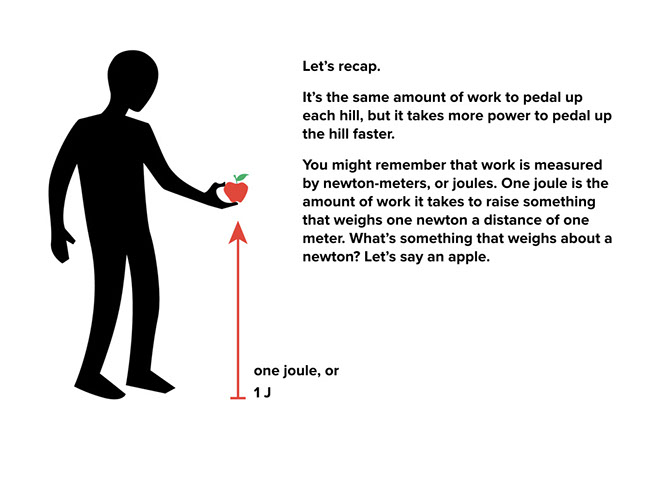

Students are first reminded the unit of measure for work is a joule. The amount of work to ride up the hill is estimated in context of the work of lifting an apple onto a shelf. The estimate is 10,000 joules.
Students are then asked to think about the work involved for both hill-climbing situations. The ratio of work to time is discussed. The ratio is first written using the word “to” and then as a fraction. Ask students to recall what a rate that has 1 in the denominator is called (unit rate). Ratio, rate, and unit rate are generally 6th and 7th grade concepts so they should be understood in this context.
Emphasize that by dividing numerator by denominator the answers will have a 1 in the denominator, so the unit rates can be compared. The goal is to determine which is greatest. Before calculating the unit rate, ask students to estimate their answers and choose which number will be greater.

Introducing watt (15 minutes)
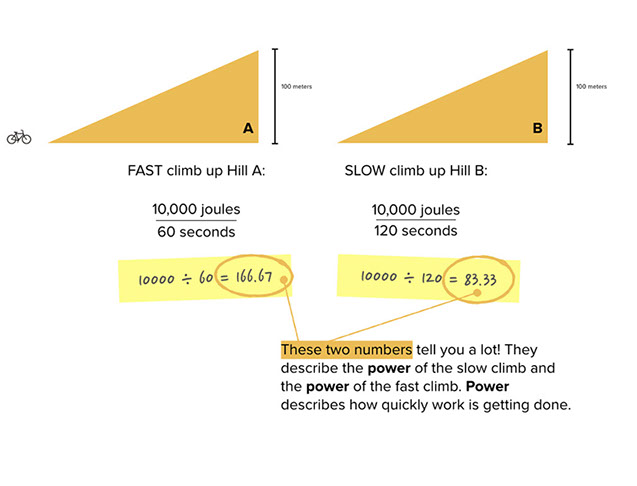

The calculations to determine which climb required the greatest power are shown at the top of this page. The two resulting unit rates can be compared because both have 1 in the denominator.
- 10,000 joules / 60 seconds or 166.67 joules / 1 second is greater than 10,000 joules / 120 seconds or 83.33 joules / 1 second. Therefore it takes twice as much power to ascend the first hill.
Pause to clarify any questions. Reiterate that a watt is a unit of measure of power, and that watt is a unit rate (1 watt = 1 joule per 1 second).
Before reading the second slide, ask students if they know how many watts are in a typical light bulb. This wattage will provide a point of reference for the definition and size of the units. Consider asking, if a windmill generates 1,000,000 watts, how many typical light bulbs could it light up?
Apply power concept to other situations (10 minutes)
BETA Version - Please send comments and corrections to info@serpinstitute.org
